Maths Page

Term 4, Week 8 - Movie Night
John, Jo and Chris have got seats for the movies. In fact their seats are F5, F6, F7. In how many ways can they sit in those seats?
Extension: If Bob turned up and sat in F8 then how many different ways could they sit?

4, Week 7 - Rawiri's Weights
Rawhiri has found some old fashioned scales where you put metal weights on one side and the fruit or vegetables on the other.

Unfortunately, he has found only three weights.
But he is still able to weigh exactly any whole number of kilograms from 1kg to 13kg.

What are the weights and how does he do the weighing?

Term 4, Week 5 - Palindrome Problem

A number is called a palindrome if it is read the same way forwards and backwards.  For example 121 or 32123 are palindromes.
The odometer (which measures the distance travelled by a car) shows a palindrome below.

What number will be the next palindrome to appear on this car’s odometer?

5

Term 4, Week 4 - Magic Squares


Put these numbers:  1, 2, 3, 4, 5, 6, 7, 8 9 into this square so that all the rows, columns, and diagonals add up to the same number.

Term 4, Week 3 - Carpark Confusion

What is the number of the missing carpark?


Term 4, Week 2 - Shake Hand Man

Six business people meet for lunch and shake hands with each other.

How many handshakes are there?

Extra for Experts - What if one of the people was the legendary 'Shake Hand Man'?  He insists on shaking hands with each person 20 times at least.  What would be the minimum amount of hand shakes that would take place at this weird business meeting then?

Term 4, Week 1 - Thousand Seconds

What time is it now?

What will the time be in a thousand seconds?

Term 3, Week 8 - Timing Tim

It’s 7km from Tim’s house to where his Grandma lives and he has to cycle there to drop off her hearing aids.
It’s uphill on the way there so he can only cycle at 14kph but he can do 21kph on the way back.

Tim leaves his house at 6pm.
How long can he stop at his Grandma’s house if he wants to be back home for his favourite TV programme at 7pm?

Term 3, Week 6 - Through the Window

In a particular shop, the price of windows is calculated according to the area of glass used and the length of frame needed.

In the picture below, glass costs £10 for an area of one small square, plus £5 for every square edge of frame.

 

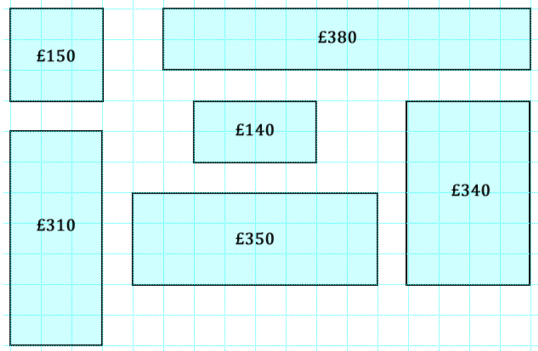
If we call the area of the glass A and the perimeter of the window P, how would you express the cost of the window in terms of A and P?

Use your formula to find pairs of rectangular windows that are different sizes but cost the same.


Term 3, Week 5

Here is a 100 square with some of the numbers shaded:

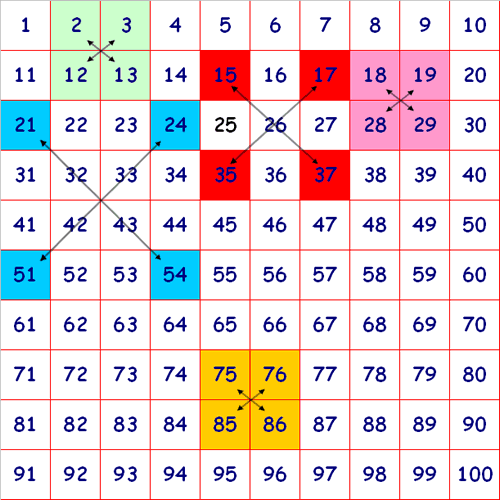
Look at the green square which contains the numbers 2,3,12 and 13.
Do you notice anything about the sum of the numbers that are diagonally opposite each other?

Look at the pink square.
What happens this time when you look at the numbers diagonally opposite each other?
What about the yellow square?
You could try with other squares which have four numbers in them.
Can you find a reason why what you notice, happens?


Look at the squares shaded red. They form the corners of a large 3 by 3 square.
If you add the numbers diagonally opposite each other, what do you notice with this larger square?
Can you find a reason why what you notice, happens?

What happens for squares of different sizes?


Term 3, Week 2

Reflection, Rotation & Translation

Term 3, Week 1

Toni is selling caps for the basketball club. The picture shows the number of caps that Toni sold during the first three weeks.

Week 1	* * * * * * * * *
Week 2	* * * * * *
Week 3	* * *
Week 4	?

How many hats must Toni sell in week 4 so that the average number of caps that she has sold per week is 7?

Extension for experts - How many more would Toni then have to sell in Week 5 so that her average number of caps per week is 8.8?

Term 2, Week 10 - Crack the Code
Follow the link below to find your POW.  You need to complete the puzzle by cracking the code.  Note the solution is at the side of the page but challenge yourself to not use it!
https://nrich.maths.org/6554


Term 2, Week 9 - Find the Value Part 2

Can you work out the value of the shapes in the box?  Use what you learnt from last week's problem to help you...

Term 2, Week 8 - Find the Value
What is the value of the shapes below.  The sum of the rows is given for a few.  See if you can use these as clues to work out the value of all the shapes...

Term 2, Week 5 - Mean, Median, Mode
What is the mean of the following numbers?
10, 39, 71, 39, 76, 38, 25

What is the median of the following numbers?
10, 39, 71, 42, 39, 76, 38, 25

What is the mode of the following numbers?
12, 11, 14, 10, 8, 13, 11, 9


Numberless Word Problems

Term 2, Week 4 - GOAL!!!

In last Friday’s netball game, Katie and Sarah scored all the goals for the Gold team. 

What Math do you see? What relationships do you see?

In last Friday’s netball game, Katie and Sarah scored all the goals for the Gold team.  How many points did the Gold team score all together?

Does this change what we know? What does this tell us? What else do you want to know?

In last Friday’s netball game, Katie and Sarah scored all the goals for the Gold team. Sarah shot ¼ of all the goals. Katie also shot goals. How many points did the Gold team score all together?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

In last Friday’s netball game, Katie and Sarah scored all the goals for the Gold team. Sarah shot ¼ of all the goals. Katie shot 12 goals. How many points did the Gold team score all together?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Extension - If that total was 5% of the team's season total then how many points did the team score all season?

Term 2, Week 3 - Money Money Money....Money

Mary had some money.

What Math do you see? What relationships do you see?

Mary had some money. She exchanged it with her brother Sam.

Does this change what we know? What does this tell us? What else do you want to know?

Mary had a $ note. She exchanged it with her brother Sam for some coins. 
What is the largest and smallest number of coins that Sam could have given Mary?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

Mary had a $5 note. She exchanged it with her brother Sam for some coins.
What is the largest and smallest number of coins that Sam could have given Mary?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Extension - If Mary lost three-quarters of her money at school how much would she have left?

Term 2, Week 2 - Pirate Problems

On the pirate ship there are pirate swords. Each pirate has swords.

If some pirates lost a sword in battle and some of the pirates each gained a new sword, how many swords would there now be on the pirate ship? _____________

What Math do you see? What relationships do you see?

On the pirate ship there are pirate swords. Each pirate has swords.

If half the pirates lost a sword in battle and a quarter of the pirates each gained a new sword, how many swords would there now be on the pirate ship? _____________

Does this change what we know? What does this tell us? What else do you want to know?

On the pirate ship there are 24 pirate swords. Each pirate has swords.

If half the pirates lost a sword in battle and a quarter of the pirates each gained a new sword, how many swords would there now be on the pirate ship? _____________

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

On the pirate ship there are 24 pirate swords. Each pirate has 2 swords.
If half the pirates lost a sword in battle and a quarter of the pirates each gained a new sword, how many swords would there now be on the pirate ship? _____________

Extension
If a two-thirds of the swords were then lost how many would there be left? _____________

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 10 - Card Costs

Lee and Jamie have decided to buy their father a card for Fathers’ Day. How much does each student contribute to the card?

What Math do you see? What relationships do you see?

Lee and Jamie have decided to buy their father a card for Fathers’ Day.  Lee puts in more than Jamie. How much does each student contribute to the card?

Does this change what we know? What does this tell us? What else do you want to know?

Lee and Jamie have decided to buy their father a card for Fathers’ Day. The card is going to cost $5.95. Lee puts in more than Jamie. How much does each student contribute to the card?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

Lee and Jamie have decided to buy their father a card for Fathers’ Day. The card is going to cost $5.95. Lee puts in 35c more than Jamie. How much does each student contribute to the card?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 9 - Gulls n Worms

It has been raining. In the paddock near the school some worms have come to the surface. As you can imagine, the seagulls have started to hover overhead.

Now gulls are satisfied if they can eat an amount of worms in one sitting. How many gulls can be satisfied by the worms in the paddock?

What Math do you see? What relationships do you see?

It has been raining. In the paddock near the school some worms have come to the surface. As you can imagine, the seagulls have started to hover overhead.

Now gulls are satisfied if they can eat 11 worms in one sitting. How many gulls can be satisfied by the worms in the paddock?

Does this change what we know? What does this tell us? What else do you want to know?

It has been raining. In the paddock near the school 273 worms have come to the surface. As you can imagine, the seagulls have started to hover overhead.

Now gulls are satisfied if they can eat 11 worms in one sitting. How many gulls can be satisfied by the worms in the paddock?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

Some octopuses, some fish and a few mermaids were happily frolicking in a rock pool. Altogether there were 38 arms, 24 eyes and 8 tails all swimming in the pool.

How many mermaids were there?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Area Problem

Term 1, Week 8 - Wild Robots

This week you have a very different problem.  You must use the squared paper provided to create a robot that is exactly 50cm2 in area (see Sven's example on board).  Try and make your robot as unique as possible and remember to glue it into your maths scrap book. Use a ruler and you can do half squares if you need to.

Palindromes


A number is called a palindrome if it is read the same way forwards and backwards.  For example 121 or 32123 are palindromes.
True or False...
If you take any number and add it to its inverse (numbers reversed), it will eventually become a palindrome.

Numberless Word Problems

Term 1, Week 7 - Mermaid Maths

Some octopuses, some fish and a few mermaids were happily frolicking in a rock pool.

How many mermaids were there?

What Math do you see? What relationships do you see?

Some octopuses, some fish and a few mermaids were happily frolicking in a rock pool. Altogether there were 38 arms all swimming in the pool.

How many mermaids were there?

Does this change what we know? What does this tell us? What else do you want to know?

Some octopuses, some fish and a few mermaids were happily frolicking in a rock pool. Altogether there were 38 arms and 24 eyes all swimming in the pool.

How many mermaids were there?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

Some octopuses, some fish and a few mermaids were happily frolicking in a rock pool. Altogether there were 38 arms, 24 eyes and 8 tails all swimming in the pool.

How many mermaids were there?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 6 - Dog Gone It!

I have dogs of different ages. How old are my dogs?

What Math do you see? What relationships do you see?

I have dogs of different ages. I add there ages together and multiply them to get two different answers. How old are my dogs?

Does this change what we know? What does this tell us? What else do you want to know?

I have dogs of different ages. If I add their ages together I get 15.  How old are my dogs?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

I have three dogs of different ages. If I add their ages together I get 15. If I multiply their ages together I get 45. How old are my dogs?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Extension - If I feed my dogs on a percentage of a dog food can based on their ages what percentage of the can of dog food would each dog get per day?

Term 1, Week 5 - Park It Up!

In parking meters, downtown, you can get parking. Dad put coins into the parking meter. At what time did the parking meter expire?

What Math do you see? What relationships do you see?

In parking meters, downtown, you can get parking for 10c. Dad put a 20c and a 50c piece into the parking meter. At what time did the parking meter expire?

Does this change what we know? What does this tell us? What else do you want to know?

In parking meters, downtown, you can get parking for 10c. Dad put a 20c and a 50c piece into the parking meter at 3.15pm. At what time did the parking meter expire?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

In parking meters, downtown, you can get 15 minutes parking for 10c. Dad put a 20c and a 50c piece into the parking meter at 3.15pm. At what time did the parking meter expire?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 4 - Jackie P and the Broken Watch

Jackie P bought a cheap watch.

What Math do you see? What relationships do you see?

Jackie P bought a cheap watch. Unfortunately for Jackie P it gained more minutes every day!

Does this change what we know? What does this tell us? What else do you want to know?

Jackie P bought a cheap watch. Unfortunately for Jackie P it gained more minutes every day! If Jackie P set his watch at noon one day, how long would it be before it next correctly showed 12 o’clock again?

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

Jackie P bought a cheap watch. Unfortunately for Jackie P it gained 30 minutes every day! If Jackie P set his watch at noon one day, how long would it be before it next correctly showed 12 o’clock again?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 3 - The Marshmallow Dilemma

On a camping trip there are marshmallows to be shared among the campers. Some campers do not want marshmallows.

What Math do you see? What relationships do you see?

On a camping trip there are 96 marshmallows to be shared among the 15 campers. Some campers do not want marshmallows.

Does this change what we know? What does this tell us? What else do you want to know?

On a camping trip there are 96 marshmallows to be shared among the 15 campers. 3 of the campers do not want marshmallows.

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

On a camping trip there are 96 marshmallows to be shared among the 15 campers. 3 of the campers do not want marshmallows. How many marshmallows will each camper get?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?

Term 1, Week 2 - The Toad, The Snake and the Dragonfly Feast

A toad ate some dragonflies. A snake ate more dragonflies than the toad.

What Math do you see? What relationships do you see?

A toad ate 41 dragonflies. A snake ate more dragonflies than the toad.

Does this change what we know? What does this tell us? What else do you want to know?

A toad ate 41 dragonflies. A snake ate 38 more dragonflies than the toad.

What knew information do you see? How does it change your understanding of the problem? So what questions could I ask myself about this problem?

A toad ate 41 dragonflies. A snake ate 38 more dragonflies than the toad. How many dragonflies did the snake eat?

Now that I have read each piece of the problem and made sense of it, how can I solve the problem?